Two equations at the heart of all macro models have the wrong sign. This is the first one (in the clearest form I can find):[1]
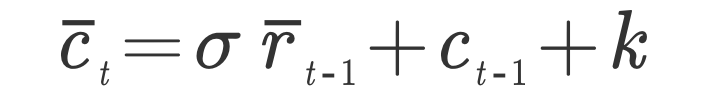
If you don’t like equations at all, ignore it. If you do, the following from the Reserve Bank of New York provides a far more complex version which is used in one of their DSGE models.[2] Either way, the message is simple. In fact, we can learn more about this problem if we stick to plain English.
When Ben Bernanke was first criticised by the hedge fund manager David Einhorn about the self-defeating effects of ever-lower interest rates, my initial reaction was to side with Bernanke and view Einhorn as a crank. Einhorn argued that initially cutting interest rates is a good idea in the face of weak demand, but at some point it becomes counter-productive. He used the analogy of eating jelly doughnuts. To summarise: at a certain point you get sick.
But the more I reflect on the effects of lower interest rates, I think the view of economists is complacent. The effects of rates cuts when interest rates are already very low may be fundamentally different to the effects when rates are high. In fact, this now seems so obvious.
Let’s revisit how economics tends to treat the relationship between consumption and interest rates. The “inter-temporal substitution of consumption” is an idea which the English-speaking world attributes to the great US economist, Irving Fisher (and European economists to Eugen Bohm-Bawerk and others). Fisher made clear that one function of interest rates is payment for postponing consumption.
In a two-period world where people work in the first period and retire in the second, how much they save, and the interest they receive, determines their consumption in retirement. Economic theory usually goes further than this and views interest rates as a “price” which equilibrates consumption through time (and its counterpart, savings) with investment – the demand for savings, which is also influenced by the real interest rate.
Now it is wise to be sceptical about the equilibrating force of real interest rates. After all, when Keynes systematically attacked the idea of macro-level market-clearing he focused on two markets: the market for savings and investment, and the labour market. He was right on both counts. The truth is there is no “price” that brings these markets into equilibrium: they are completely different to markets for other goods and services.
But before we get to how it might all break down, let me first try and outline the optimistic, “equilibrium” view.
Continuing with the two period example above, there is a sense in which interest rates can be made to look like a “price”: interest rates are the opportunity cost of consumption, so if they rise I have a greater incentive to consume less, and save more. That starts to sound like a supply curve of savings – price (interest rates) goes up, supply increases. That’s appealing, particularly if it is also plausible that the relationship of interest rates to investment is the opposite.
That is a very, very old view of how the market for savings and investment works, and for all their clever new techniques, it is pretty much what virtually all modern macroeconomic models assume. Consider this summary from the New York Fed on how their whiz-bang DSGE model of the US economy predicts changes in demand in response to interest rates:
“According to this so-called Euler equation, desired consumption decreases when the (gross) real interest rate increases … this framework is similar … to a traditional IS equation, since it describes the relationship between aggregate activity and the ex ante real interest rate, which must hold for the final-good market to clear. Unlike a traditional IS relationship, though, this equation is dynamic and forward looking [wow], as it involves current and future expected variables. In particular, it establishes a link between current output and the entire [really?] future expected path of real interest rates …
Through this channel, expectations of future monetary policy directly affect current economic conditions. In fact, this equation shows that future interest rates are just as important to determine today’s output as the current level of the short-term rate, as we describe in our discussion of the role of policy expectations.
In our full model, the Euler equation is somewhat more complicated … because of the consumption habit, which is a source of richer, and more realistic, output dynamics in response to changes in the interest rate. Nevertheless, these more intricate dynamics do not change the qualitative nature of the relationship between real rates and demand.”
We’ll keep it simple: when current and expected future interest rates fall, consumption spending rises.
The sign is wrong
One of the problems with the sort of complex modeling that the New York Fed and others are trying to achieve, is that the formal mathematical difficulties are such that it is easy to lose sight of the wood. Einhorn stuffing his face with doughnuts and concocting new theories is not really troubled by the modeling. In math-jargon, he is suggesting not only that the relationship between interest rates and desired consumption is non-linear, but the sign of the correlation may change when rates get really low. He is also saying that the marginal utility of consumption might matter – the doughnut analogy isn’t entirely spurious.
To think about this almost-rigorously, it helps to look at the factors behind the Euler equation, or specifically, the determinants of the interest rate elasticity of the inter-temporal substitution of consumption. That’s a mouthful.
Let’s simplify: Whenever the price of something changes there are two effects – an income and a substitution effect. If the price of gas falls it becomes cheaper relative to other things (the substitution effect) but also people’s real disposable income rises, which also effects their spending behavior.
If interest rates rise, the “substitution effect” has a negative sign on consumption: the opportunity cost of consumption in period one has risen, this encourages us to save more and consume less.
The magnitude of this effect is likely to vary significantly depending on the starting point level of real interest rates. A consumer who has been credit-constrained and experiences a fall in real interest rates will borrow more for consumption. If interest rates are very high and there is pent-up demand for consumer durables and housing, interest rate cuts may well spur consumption booms. We have seen this in recent years across many emerging economies as global real interest rates have fallen.
But the prevailing conditions in the developed world are the opposite. The US economy is in part recovering from a boom in lending to people on low incomes. The availability of credit – particularly in housing – is not favourable for those with the highest propensity to consume. It is likely that the substitution effect of a fall in the opportunity cost of consumption has diminished. It may be close to zero. [3]
What about the income effect? I suspect this is where Einhorn has a really powerful case. The marginal utility of consumption is important – if current consumption is already high, the marginal utility in period 1 will be low – and if people are worried about longevity and the rising costs of healthcare in old age, marginal utility in period 2 will be high. The savings preferences of those on middle- to high-incomes may be very resistant to further declines in real interest rates.
Think about a rule-of-thumb people use in planning for retirement. Choose a reasonable level of retirement income and divide that by the yield on a 10-year treasury – (to keep the math simple, also assume that you want to bequeath the full capital value of your savings to children, charity, or the state).
Ok, if the yield on the 10-year treasury is 5% and $50,000 is your target income, you need $1,000,000 dollars of savings. Now do you save more or less if the yield on 10-year treasuries falls to 2.5%? You save more – that’s the income effect.
There is a very good chance that when interest rates are already low and the yield curve is offering little to those planning for retirement, when long-term costs of health care and longevity are rising, when credit conditions are far from easy for the young and those on low incomes, when there is little evidence of pent-up demand for durables, housing or consumption, that the sign in the Euler equation has changed. Reductions in interest rates or interest rate expectations around these levels don’t boost consumption – they boost desired savings.
Sorry sophisticated model-builders, the jelly doughnut-eating, economically illiterate, hedge fund guy may be on to something.
You may be reading all of this and thinking, “Who cares? This is just another angle on secular stagnation, which everyone is talking about.” Part of secular stagnation is that lower real rates lose their potency. But no policymakers or mainstream modelers are arguing that the sign between real interest rates and desired savings has changed (in fairness to Larry Summers, he’s getting close). Consider this discussion at the New York Fed. But a change in the sign has critical policy implications: if you are worried about insufficient demand, negative nominal interest rates and higher inflation targets to bring real interest rates lower, may backfire. Lower real interest rates may actually make the problem worse.
This has a very significant bearing on contingency planning for policymakers. We may be in the middle of a sustained global recovery which allows real interest rates to gradually rise. But we may not. In which case, if lower real interest rates potentially make matters worse, we need alternative policies. A change in attitudes towards fiscal policy is one option as Krugman, Summers, DeLong and Wren-Lewis have argued. New tools for central banks is the other.
[1] It’s a consumption Euler equation, introduced originally by Hall. Noah Smith has an excellent post on the empirical question marks. In the form presented here, it shows that the expected change in the log of consumption is a parameter, sigma, times the expected real return on savings, plus a constant. In a two period world, t and t-1, if sigma is positive a higher expected interest rate in the current period, t-1, reduces current period consumption and raises consumption in the second period, t. All central bank models assume sigma is positive – despite empirical evidence, which is inconclusive regarding its sign and magnitude. There is a very clear Fed paper by Doug Elmendorf on the subject. In consumer theory, the consumption Euler equation is derived as a result of a consumer’s attempt to maximise the utility of consumption over a lifetime subject to the budget constraint of life-time income. What it shows is that one conclusion of this optimisation exercise is that the expected change in consumption at any point in time, t, is a function of the sensitivity of the inter-temporal substitution of consumption to the expected real return on savings. This chapter on consumption by Charles Jones at Sanford is an excellent introduction. In consumer theory the overall effect of a change in interest rates is not fully captured by the Euler equation, but by a shift in the budget constraint through wealth and income effects, as this short note by Thijs van Rens shows. For the purposes of this blog, I am viewing this equation as an empirical hypothesis regarding the sensitivity of consumption to real interest rates – so I consider both income and substitution effects.
[2] Page 4
[3]The empirical literature is very clear that household circumstances can change the sign of interest rate sensitivity. Some of the most interesting research has been done by Christopher Carroll formerly an economist at the Federal Reserve, now a professor at John Hopkins University. This interview is excellent, as is this paper – declaring death to the consumption Euler equation.

Perhaps the speed and size of interest rate changes also matters.
In April 2008 UK bank rate was 5%. Less than a year later, it was 0.5%.
Perhaps interest rate changes of this size in a short period simply send the message “We’re in a mess!”, and cause consumers to become more cautious.
I remember pointing out to some work colleagues in 2009 that because of the rate changes they had substantially more disposable income because of reduced mortgage payments. They were therefore better off than in 2008 and should be happily spending these gains.
They weren’t convinced……
I think you have a point, and the UK system is more responsive to short-term interest rates than most, precisely because of variable rate mortgages. But as you approach zero and as the yield curve flattens at such low levels the effects are perverse and the income effect may dominate.
But do you save less for retirement when Treasury yields fall, given that your whole asset base is then revalued higher (& across asset classes)? You immediately move closer to your capital target (less urgency to save aggressively – not more) and you’re bolstered by a wealth effect. Not convinced your average man on the street watches bond yields closely enough to save more when they fall – but they might notice the pension value rise…?
Possibly, Harry. But bear in mind pensions don’t necessarily rise in value when gilt yields fall, because present value of liabilities rises. I think it depends: if you are redeeming capital to purchase goods and services higher capital values benefit you. But if you are a net saver you should prefer to invest at higher yields.
Apologies for digging this out from the archive, but it’s arguably still highly relevant…
Considering a case of falling interest rates the standard decomposition yields the following:
Substitution effect: bringing forward consumption regardless of borrower/lender status; let’s assume the case most favourable to opponents of NIRP, i.e. that the substitution effect is zero.
Income effect: for *savers* this is negative (although Harry has a point as far as those with a positive duration gap are concerned), but for borrowers it is positive, as they pay less to refinance their debt etc.
So for the total effect to be negative, the (negative) income effect for savers would have to outweigh the (positive) income effect for borrowers. And since the marginal propensity to consume is higher for the latter, this seems unlikely even if we consider an economy with a balanced private sector account (such that domestic borrowing=domestic lending)…
What am I missing?
Thank you,
Lukas
[…] induce us to spend more and save less. Yet Mr Carney has good reasons to be cautious: there is concern among economists about the impact of ever-lower rates on the global banking […]
[…] induce us to spend more and save less. Yet Mr Carney has good reasons to be cautious: there is concern among economists about the impact of ever-lower rates on the global banking […]
[…] induce us to spend more and save less. Yet Mr Carney has good reasons to be cautious: there is concern among economists about the impact of ever-lower rates on the global banking […]
[…] In standard economic theory, interest rates are the price we pay for instant gratification: lower rates induce us to spend more and save less. Yet Mr Carney has good reasons to be cautious: there is concern… […]
[…] induce us to spend more and save less. Yet Mr Carney has good reasons to be cautious: there is concern among economists about the impact of ever-lower rates on the global banking […]
[…] have argued elsewhere that real private consumption spending is not a straightforward negative function of real interest […]
[…] In un altro articolo sostenevo che la spesa per i consumi privati reali non fosse una funzione negativa diretta dei tassi di interesse reali. Il grafico seguente mostra come la relazione sia cambiata negli ultimi 40 anni negli Stati Uniti. Anche se sembra esserci una relazione negativa all’inizio del periodo, essa è meno chiara oggi. […]
[…] hatte bereits an anderer Stelle argumentiert, dass die privaten Konsumausgaben nicht einfach eine negative Funktion der […]
[…] En el pasado ya he sostenido que el gasto real del consumo privado no guarda una relación inversa directa con los tipos de interés reales. El siguiente gráfico muestra cómo la relación ha cambiado en los últimos cuarenta años en los EE.UU.. Aunque no parece haber una relación negativa al comienzo del periodo, dicha relación es mas clara hoy en día. […]
[…] Mr. Rajan added that the public may choose to look through current “unnatural” asset price inflation induced by unconventional monetary policies and instead exercise prudence in risk management on concerns of future volatility. He was not alone to focus on the starting point in rates to gauge rate cuts’ impact on consumption, for hedge fund manager Eric Lonergan also outlined a case which substitution effect of a fall in the opportunity cost of consumption has diminished in the developed…: […]
[…] Mr. Rajan added that the public may choose to look through current “unnatural” asset price inflation induced by unconventional monetary policies and instead exercise prudence in risk management on concerns of future volatility. He was not alone to focus on the starting point in rates to gauge rate cuts’ impact on consumption, for hedge fund manager Eric Lonergan also outlined a case which substitution effect of a fall in the opportunity cost of consumption has diminished in the developed…: […]
[…] Mr. Rajan added that the public may choose to look through current “unnatural” asset price inflation induced by unconventional monetary policies and instead exercise prudence in risk management on concerns of future volatility. He was not alone to focus on the starting point in rates to gauge rate cuts’ impact on consumption, for hedge fund manager Eric Lonergan also outlined a case which substitution effect of a fall in the opportunity cost of consumption has diminished in the developed…: […]
[…] Mr. Rajan added that the public may choose to look through current “unnatural” asset price inflation induced by unconventional monetary policies and instead exercise prudence in risk management on concerns of future volatility. He was not alone to focus on the starting point in rates to gauge rate cuts’ impact on consumption, for hedge fund manager Eric Lonergan also outlined a case which substitution effect of a fall in the opportunity cost of consumption has diminished in the developed…: […]
A few years late on this thread, but…
If the sign did flip and the guy eating doughnuts got sick, how long until it flips back and he reaches for another? How long does a rising rate spur spending and when does it begin to disincentivize consumption once again?